Building External Connections in Mathematica
This builds off of something I brought up on StackExchange a bit ago as well as some recent work I’ve done in building a nicer interface to Git and GitHub .
I’m hoping to mainly lay out in a brief fashion how one can tackle the really broad question of how to build interfaces and what tricks can be used to make them nice.
There are many possible classifications for these types of interfaces, but the major two I’ve run into are:
-
Restricted interfaces
by this I mean interfaces where there is a proscribed set of functionality the interface should implement. Examples of this include APIs, CLI tools, and some packages. -
Unrestricted interfaces
by this I mean interfaces where there is a highly-flexible set of functionality that we want to implement. The major example of this is programming languages.
I’ll discuss the restricted case first as it’s much easier to handle
Restricted Interfaces
Git
When linking to Git there’s a very small set of commands you really need to include. You can pretty much just look at the git book and determine what you need to include.
Once you’ve done that, all you really need to do is write a general-purpose wrapper function for running Git and then register a bunch of different functions that do minor work on top of that.
I put this into a subpackage of my main application . You can go there for all the details. In essence, though, I just wrote a bunch of little functions to handle different parts of the Git process. For example, here’s how I registered the GitAdd function:
GitRegisterFunction[GitAdd, "add",
{
"DryRun"->"dry-run",
"Verbose"->"verbose",
"Force"->"force",
"Interactive"->"interactive",
"Patch"->"patch",
"Edit"->"edit",
"Update"->"update",
"NoIgnoreRemoval"->"no-ignore-removal",
"IgnoreRemoval"->"ignore-removal",
"IntentToAdd"->"intent-to-add",
"Refresh"->"refresh",
"IgnoreErrors"->"ignore-errors",
"IgnoreMissing"->"ignore-missing",
"NoWarnEmbeddedRepo"->"no-warn-embedded-repo",
"ChangeModee"->"chmod"
}
]
This just defines the function GitAdd , the git command to call "add" , and the way to map Mathematica options to Git options.
Once I had all the functions I wanted I cooked them into a single Association to act as a router from a name to a method:
$GitActions=
<|
"Create"->
GitCreate,
"Init"->
GitInit,
"Clone"->
GitClone,
"AddGitIgnore"->
GitAddGitIgnore,
"AddGitExclude"->
GitAddGitExclude,
"Add"->
GitAdd,
"Move"->
GitMove,
...,
"Archive"->
GitArchive,
"SVN"->
GitSVN,
"Bundle"->
GitBundle,
"Daemon"->
GitDaemon,
"Help"->
GitHelp,
"HelpSynopsis"->
GitHelpSynopsis,
"HelpDescription"->
GitHelpDescription,
"HelpOptions"->
GitHelpOptions,
"HelpFlags"->
GitHelpFlags,
"HelpFlagMap"->
GitHelpFlagMap
|>;
And I define a single function that provides the true interface to Git. I called that one Git . Then you can define it (with unnecessary parts excised) like:
Git[
command_?(KeyMemberQ[$gitactions,ToLowerCase@#]&),
args___
]:=
With[{cmd=$gitactions[ToLowerCase[command]]},
With[{r=cmd[args]},
r/;Head[r]=!=cmd
]
];
And even better you can add autocompletions and things to make it easy to know what’s there to use. E.g.:
<<BTools`External`
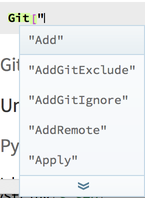
And then can do things like:
Git["HelpDescription", "rm"]
-----------Out-----------
"Remove files from the index, or from the working tree and the index.\ngit rm will not remove a file from just your working directory. (There\nis no option to remove a file only from the working tree and yet keep\nit in the index; use //bin//rm if you want to do that.) The files being\nremoved have to be identical to the tip of the branch, and no updates\nto their contents can be staged in the index, though that default\nbehavior can be overridden with the --f option. When ----cached is given,\nthe staged content has to match either the tip of the branch or the\nfile on disk, allowing the file to be removed from just the index."GitHub
In that package I do a similar thing for GitHub’s API, except with the important exception that the default operation for each registered function isn’t to actually call the API but rather to build the HTTPRequest that the function will actually use.
Unrestricted Interfaces
Python
I developed a package for linking to python that I called PyTools .
To marshal Mathematica code down to a python representation I built out a symbolic Python package . This type of symbolic conversion is a powerful way to build an interface. In it Mathematica constructs are reduced to an intermediate symbolic representation which Mathematica can still easily manipulate and then further processing directions are defined on this symbolic form.
As an example, we’ll see how I did it for this package. First load the package:
<<PyTools`Symbolic`
Then you can take a Mathematica expression and convert it into a symbolic representation of a python expression. In general this is set up so your write python-like code in Mathematica:
ToSymbolicPython[
Import["PIL"];
img=PIL.Image[];
img.show[]
]
(*Out:*)
PyColumn[{PyImport["PIL"],PyAssign[PySymbol["img"],PyDot[PySymbol["PIL"],PySymbol[Image][]]],PyDot[PySymbol["img"],PySymbol["show"][]]}]
And we can see that this has built out a rather complicates structure to represent this simple program. We’ll take it bit-by-bit:
ToSymbolicPython@Import["PIL"]
(*Out:*)
PyImport["PIL"]
This simply maps to a symbolic structure called PyImport . If we convert that to a python string:
PyImport["PIL"]//ToPython
(*Out:*)
"import PIL"
It just registers an import statement. In fact this uses Sow to make sure the import occurs at the header of the file. This is just generally good practice.
Moving onto the next piece
ToSymbolicPython[img=PIL.Image[]]
(*Out:*)
PyAssign[PySymbol["img"],PyDot[PySymbol["PIL"],PySymbol[Image][]]]
This builds out a symbolic representation of this syntax. It’s inspired by the low-level representation Mathematica uses:
FullForm@Hold[img=PIL.Image[]]
(*Out:*)
Hold[Set[img,Dot[PIL,Image[]]]]
We have a syntactic wrapper for assignment ( Set ) for the . accessor in python, and a conversion of Mathematica Symbol constructs into PySymbol constructs which have less ambiguity in conversion to a string.
Finally, taking this all together, we have a PyColumn expression which is just a mimic of Mathematica’s Column function which arranges pieces line-by-line after each other. And this gives a nice way to go from Mathematica-level syntax to python code:
ToSymbolicPython[
Import["PIL"];
img=PIL.Image[];
img.show[]
]//ToPython
(*Out:*)
"import PIL\nimg = PIL.Image()\nimg.show()\n"
All it took was a long-symbolic detour.
As a final note, the power of this approach is in its flexibility. For instance, if we want to register new type conversions, we need only register patterns to get from a Mathematica construct to a symbolic python one. I did this for a large set of constructs, allowing one to automatically generate code for things like:
ToSymbolicPython[
myFunc[file]:=
With[{x=Open[file], y=Open[file2, "w+"]},
Do[y.write[line], {line, x}]
]
]//ToPython//StringTrim
(*Out:*)
"def myFunc(file):\n\twith open(file) as x:\n\t\twith open(file2, 'w+') as y:\n\t\t\tfor line in x:\n\t\t\t\ty.write(line)\n\t\t\t\tNone"
SymbolicC
SymbolicC is a package built into Mathematica that works in a similar way. I’ll let its documentation speak for it.
MATLink
This is a package developed by some top-tier Mathematica users to link MATLAB and Mathematica. It works on the lowest-level possible and in the most unrestricted way. This also makes it among the most powerful packages out there.
The basic idea is to use the MathLink system to pass packets around which encode the evaluation data desired. This is incredibly flexible but requires a lot of work to do right.
Hybrid Interfaces
Psi4
I won’t go into this one much, but it’s a link I provide to the software Psi4 in my main chemistry package. What makes this a hybrid interface is that the basic input for Psi4 is about 80% structured so that part can be restricted, but there is also about 20% flexibility that requires a more unstructured interface. To do this I use tricks somewhere in between what I did for Git and for Python.
Feel free to ask me more if you have comments or questions.